如果在房间的角落打开香水瓶,需要很长时间才可在房间的 相反角落处检测到芳香气体物质。这一实验似乎与前一章节 中描述的平均气体速度相矛盾。出现这种情况的原因在于气 体粒子在其飞行路途中遭受大量的碰撞。平均自由程是粒子 在与其它粒子进行两次连续碰撞之间可移动的平均距离。
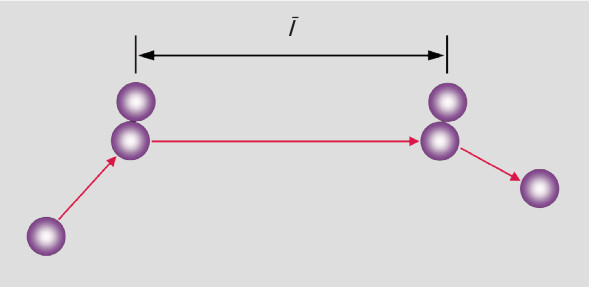
图 : 两次碰撞之间的平均自由程对于同种粒子的碰撞,平均自由程由下式计算:
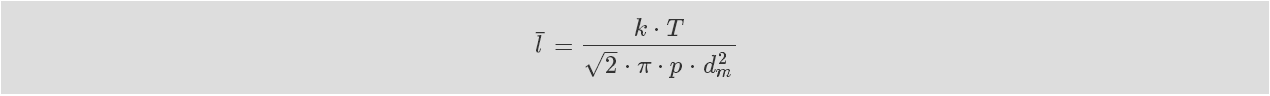
公式 : 平均自由程
| j | 平均自由程 | [m] |
| dm | 分子直径 | [m] |
从公式可看出, 平均自由程与温度成比,与压力和分子 直径成反比。 在这一点上,我们将忽略学术文献中讨论的该等 式进一步的变体, 学术文献研究了诸如不同气体粒子直径的碰 撞、 气体粒子与离子或电子的碰撞以及 温度影响等。
为说明平均自由程的温度依赖性,公式 1-11 经常书写为将温 度作为方程右边的唯一变量。
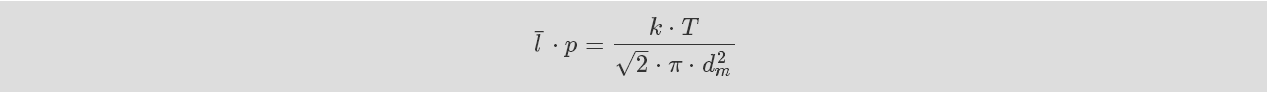
公式 : 平均自由程 II
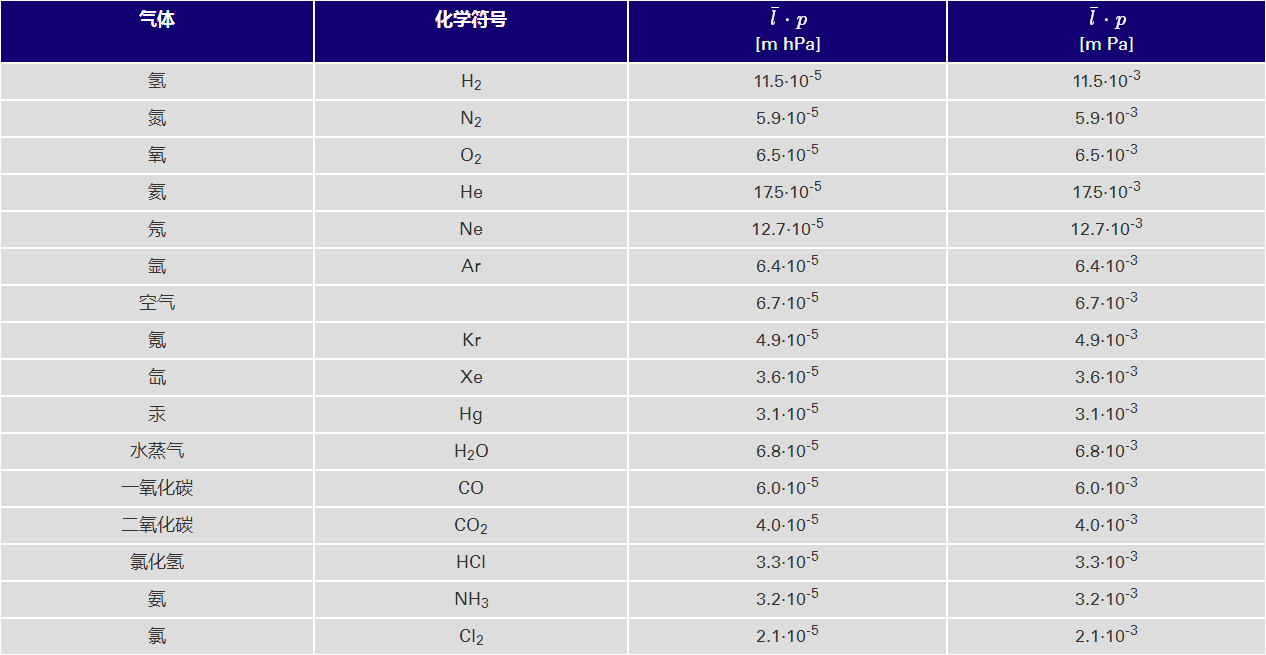
表 : 气体在 273.15 K 时的平均自由程, 显示了一些气体在 0°C 时的 j⋅p 值
使用表中的值,我们现在估算氮分子在各种压力下的 平均自由程:
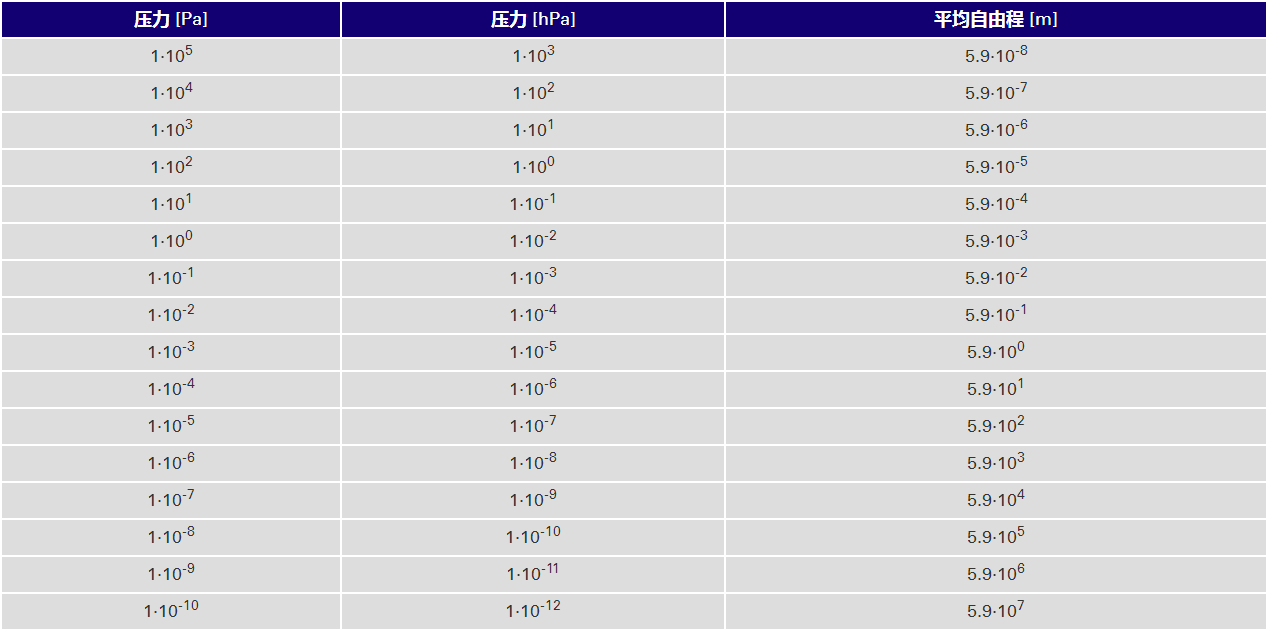
表 : 氮气分子在 273.15 K (0°C) 时的平均自由程
因在大气压下,氮分子在两次碰撞之间移动的距离为 59 nm,而在压力低于 10-8 hPa 的超高真空下,其移动的距 离为几公里。分子数密度和平均自由程的关系可以用图来表示。
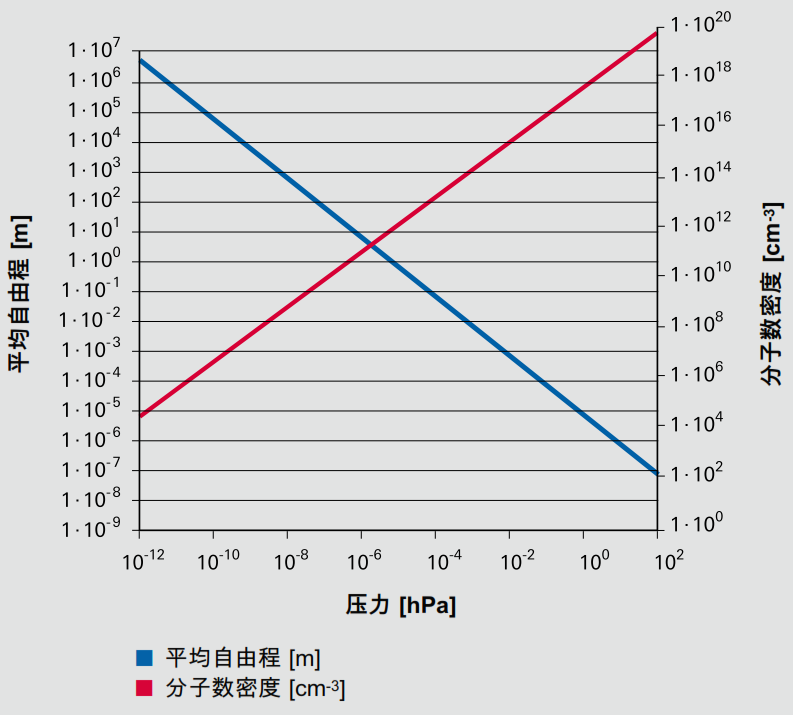
图: 氮在温度为 273.15 K 时的分子数密度(红色,右边 y 轴)和平均自 由程(蓝色,左边 y 轴)





 售前客服
售前客服